Optimal number of clusters obtained by combining mixture components

Return the optimal number of clusters by combining mixture components based on the entropy method discussed in the reference given below.

Usage

clustCombiOptim(object, reg = 2, plot = FALSE, ...)

Arguments

object: An object of class 'clustCombi' resulting from a call to clustCombi.
reg: The number of parts of the piecewise linear regression for the entropy plots. Choose 2 for a two-segment piecewise linear regression model (i.e. 1 change-point), and 3 for a three-segment piecewise linear regression model (i.e. 3 change-points).
plot: Logical, if TRUE an entropy plot is also produced.
...: Further arguments passed to or from other methods.

Value

The function returns a list with the following components:

numClusters.combi: The estimated number of clusters.
z.combi: A matrix whose [i,k]th entry is the probability that observation i in the data belongs to the kth cluster.
cluster.combi: The clustering labels.

References

J.-P. Baudry, A. E. Raftery, G. Celeux, K. Lo and R. Gottardo (2010). Combining mixture components for clustering. Journal of Computational and Graphical Statistics, 19(2):332-353.

Author

J.-P. Baudry, A. E. Raftery, L. Scrucca

Examples

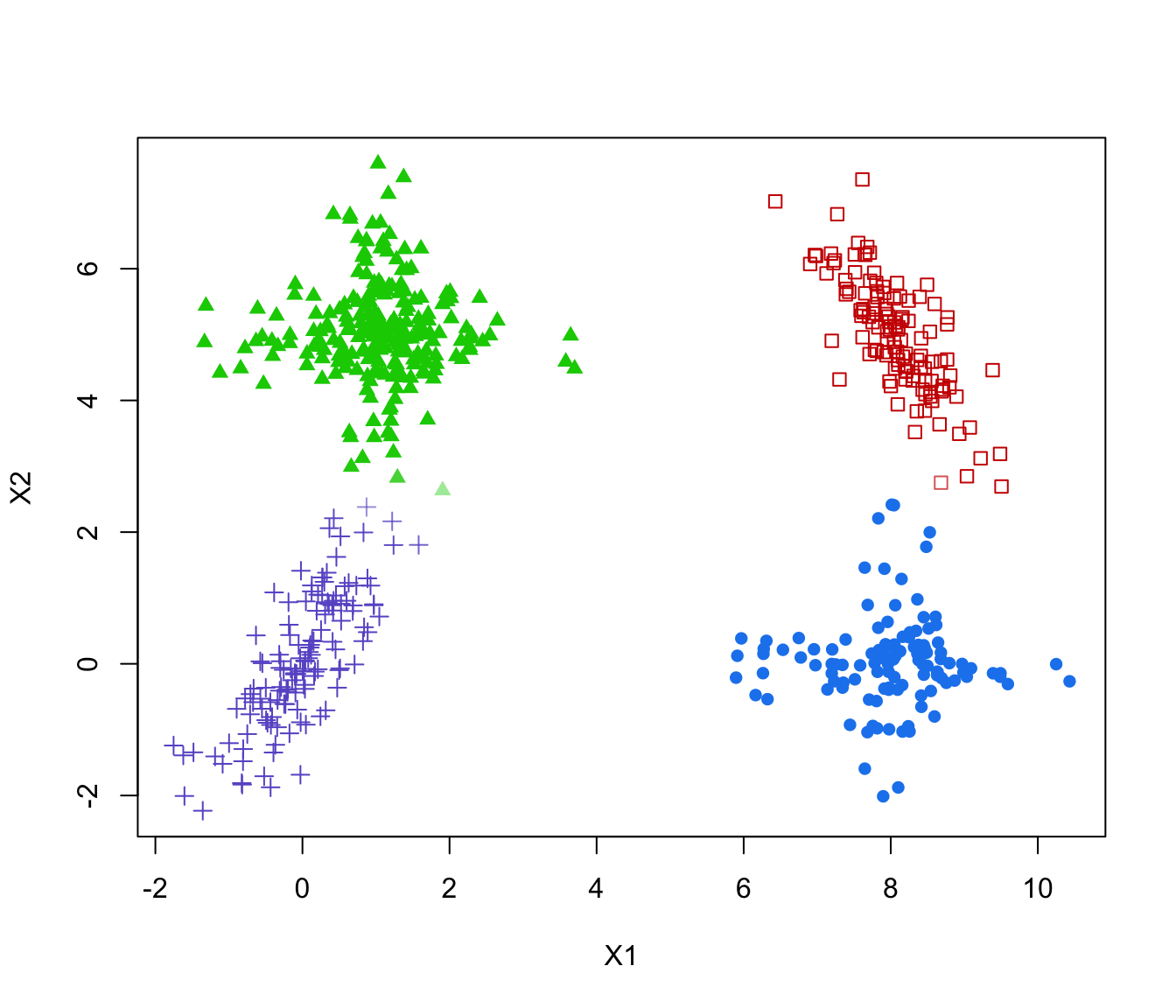
data(Baudry_etal_2010_JCGS_examples)
output <- clustCombi(data = ex4.1) 
combiOptim <- clustCombiOptim(output)
str(combiOptim)
#> List of 3
#>  $ numClusters.combi: int 4
#>  $ z.combi          : num [1:600, 1:4] 1.00 1.00 5.78e-04 1.85e-42 3.85e-35 ...
#>  $ cluster.combi    : num [1:600] 1 1 2 3 3 4 4 3 3 2 ...

# plot optimal clustering with alpha color transparency proportional to uncertainty
zmax <- apply(combiOptim$z.combi, 1, max)
col <- mclust.options("classPlotColors")[combiOptim$cluster.combi]
vadjustcolor <- Vectorize(adjustcolor)
alphacol = (zmax - 1/combiOptim$numClusters.combi)/(1-1/combiOptim$numClusters.combi)
col <- vadjustcolor(col, alpha.f = alphacol)
plot(ex4.1, col = col, pch = mclust.options("classPlotSymbols")[combiOptim$cluster.combi])