Recover parameters in the original scale

Given a GMM for bounded data, computes the means and variances in the original scale from the estimated mixture components parameters dataset using simulations.

Usage

MclustBoundedParameters(object, nsim = 1000000, ...)

Arguments

object

An object of class 'MclustBounded' or 'densityMclustBounded'.

nsim

An integer specifying the number of simulations to employ.

...

Further arguments passed to or from other methods.

Examples

# \donttest{
x = rlnorm(1000, 0, 1)
mod = densityMclustBounded(x, lbound = 0, lambda = 0)
summary(mod, parameters = TRUE)
#> ── Density estimation for bounded data via GMMs ───────────
#>            
#> Boundaries:   x
#>       lower   0
#>       upper Inf
#> 
#> Model E (univariate, equal variance) model with 1 component
#> on the transformation scale:
#> 
#>  log-likelihood    n df       BIC       ICL
#>       -1423.435 1000  2 -2860.685 -2860.685
#> 
#>                             x
#> Range-power transformation: 0
#> 
#> Mixing probabilities:
#> 1 
#> 1 
#> 
#> Means:
#>           1 
#> 0.007990182 
#> 
#> Variances:
#>         1 
#> 0.9915365 
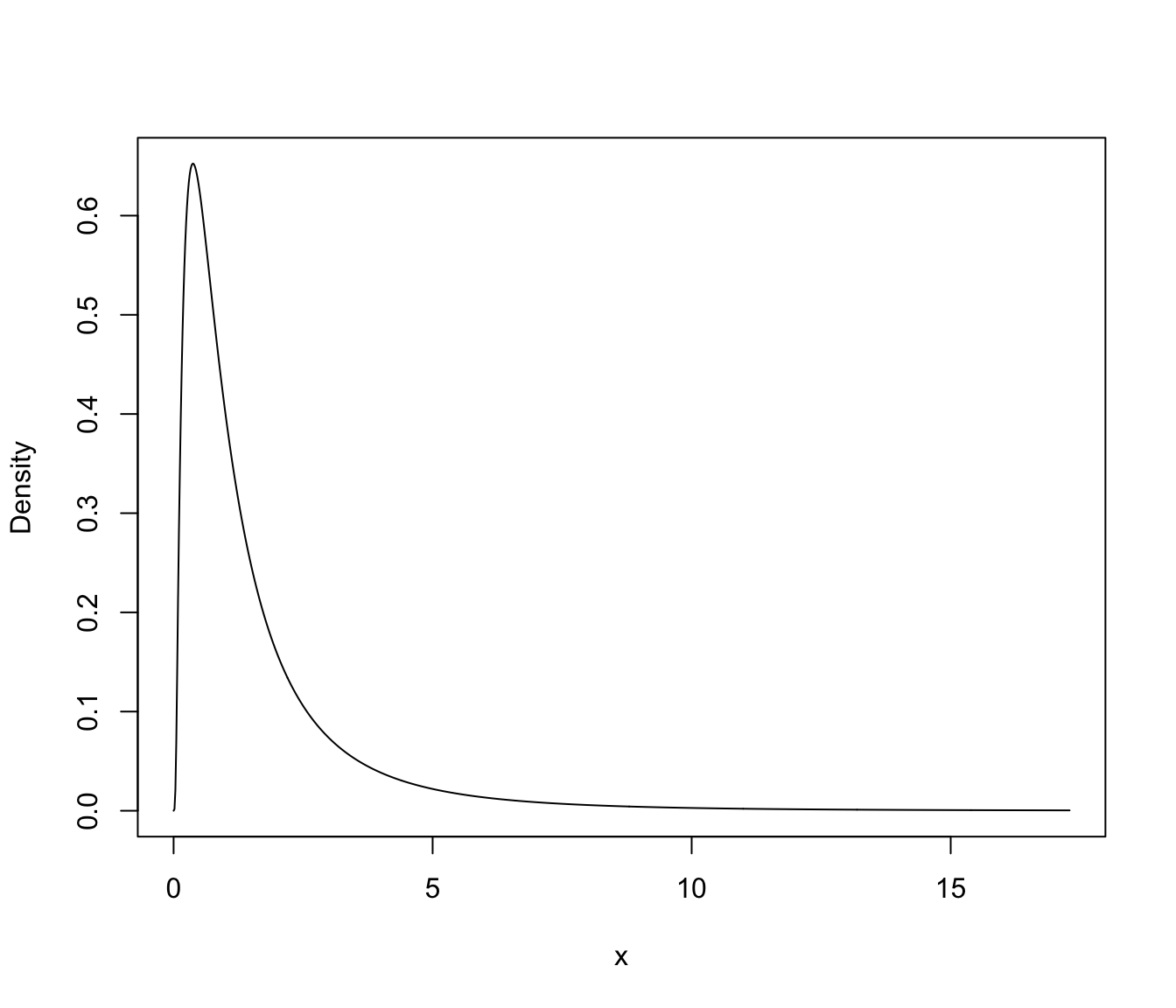
plot(mod, what = "density")

# transformed parameters (from log-normal distribution)
# mean
with(mod$parameters, 
     exp(mean + 0.5*variance$sigmasq))
#>       1 
#> 1.65493 
# var
with(mod$parameters,
     (exp(variance$sigmasq) - 1)*exp(2*mean + variance$sigmasq))
#>        1 
#> 4.643273 
# using simulations
MclustBoundedParameters(mod)
#> $mean
#>       [,1]
#> x 1.655112
#> 
#> $variance
#>       [,1]
#> x 4.561358
#> 
# }