Model-based mixture density estimation for bounded data

Density estimation for bounded data via transformation-based approach for Gaussian mixtures.

Usage

densityMclustBounded(
  data,
  G = NULL,
  modelNames = NULL,
  criterion = c("BIC", "ICL"),
  lbound = NULL,
  ubound = NULL,
  lambda = c(-3, 3),
  prior = NULL,
  initialization = NULL,
  nstart = 25,
  parallel = FALSE,
  seed = NULL,
  ...
)

# S3 method for class 'densityMclustBounded'
summary(object, parameters = FALSE, ...)

Arguments

data

A numeric vector, matrix, or data frame of observations. If a matrix or data frame, rows correspond to observations and columns correspond to variables.

G

An integer vector specifying the numbers of mixture components. By default G=1:3.

modelNames

A vector of character strings indicating the Gaussian mixture models to be fitted on the transformed-data space. See mclust::mclustModelNames() for a descripton of available models.

criterion

A character string specifying the information criterion for model selection. Possible values are BIC (default) or ICL.

lbound

Numeric vector proving lower bounds for variables.

ubound

Numeric vector proving upper bounds for variables.

lambda

A numeric vector providing the range (min and max) of searched values for the transformation parameter(s). If a matrix is provided, then for each variable a row should be provided containing the range of lambda values for the transformation parameter. If a variable must have a fixed lambda value, the provided min and max values should be equal. See examples below.

prior

A function specifying a prior for Bayesian regularization of Gaussian mixtures. See mclust::priorControl() for details.

initialization

A list containing one or more of the following components:

noise A logical or numeric vector indicating an initial guess as to which observations are noise in the data. If numeric the entries should correspond to row indexes of the data. If logical an automatic entropy-based guess of noisy observations is made. When supplied, a noise term will be added to the model in the estimation.
Vinv When a noise component is included in the model, this is a numerical optional argument providing the reciprocal of the volume of the data. By default, the mclust::hypvol() is used on the transformed data from a preliminary model.

nstart

An integer value specifying the number of replications of k-means clustering to be used for initializing the EM algorithm. See kmeans().

parallel

An optional argument which allows to specify if the search over all possible models should be run sequentially (default) or in parallel.

For a single machine with multiple cores, possible values are:

a logical value specifying if parallel computing should be used (TRUE) or not (FALSE, default) for evaluating the fitness function;
a numerical value which gives the number of cores to employ. By default, this is obtained from the function parallel::detectCores();
a character string specifying the type of parallelisation to use. This depends on system OS: on Windows OS only "snow" type functionality is available, while on Unix/Linux/Mac OSX both "snow" and "multicore" (default) functionalities are available.

In all the cases described above, at the end of the search the cluster is automatically stopped by shutting down the workers.

If a cluster of multiple machines is available, evaluation of the fitness function can be executed in parallel using all, or a subset of, the cores available to the machines belonging to the cluster. However, this option requires more work from the user, who needs to set up and register a parallel back end. In this case the cluster must be explicitely stopped with parallel::stopCluster().

seed

An integer value containing the random number generator state. This argument can be used to replicate the result of k-means initialisation strategy. Note that if parallel computing is required, the doRNG package must be installed.

...

Further arguments passed to or from other methods.

object

An object of class 'densityMclustBounded'.

parameters

A logical, if TRUE the estimated parameters of mixture components are printed.

Value

Returns an object of class 'densityMclustBounded'.

Details

For more details see vignette("mclustAddons")

References

Scrucca L. (2019) A transformation-based approach to Gaussian mixture density estimation for bounded data. Biometrical Journal, 61:4, 873–888. doi:10.1002/bimj.201800174

Author

Luca Scrucca

Examples

# \donttest{
# univariate case with lower bound
x <- rchisq(200, 3)
xgrid <- seq(-2, max(x), length=1000)
f <- dchisq(xgrid, 3)  # true density
dens <- densityMclustBounded(x, lbound = 0)
summary(dens)
#> ── Density estimation for bounded data via GMMs ───────────
#>            
#> Boundaries:   x
#>       lower   0
#>       upper Inf
#> 
#> Model E (univariate, equal variance) model with 1 component
#> on the transformation scale:
#> 
#>  log-likelihood   n df       BIC       ICL
#>       -395.2477 200  3 -806.3903 -806.3903
#> 
#>                                     x
#> Range-power transformation: 0.2376863
summary(dens, parameters = TRUE)
#> ── Density estimation for bounded data via GMMs ───────────
#>            
#> Boundaries:   x
#>       lower   0
#>       upper Inf
#> 
#> Model E (univariate, equal variance) model with 1 component
#> on the transformation scale:
#> 
#>  log-likelihood   n df       BIC       ICL
#>       -395.2477 200  3 -806.3903 -806.3903
#> 
#>                                     x
#> Range-power transformation: 0.2376863
#> 
#> Mixing probabilities:
#> 1 
#> 1 
#> 
#> Means:
#>         1 
#> 0.8645257 
#> 
#> Variances:
#>        1 
#> 1.042347 
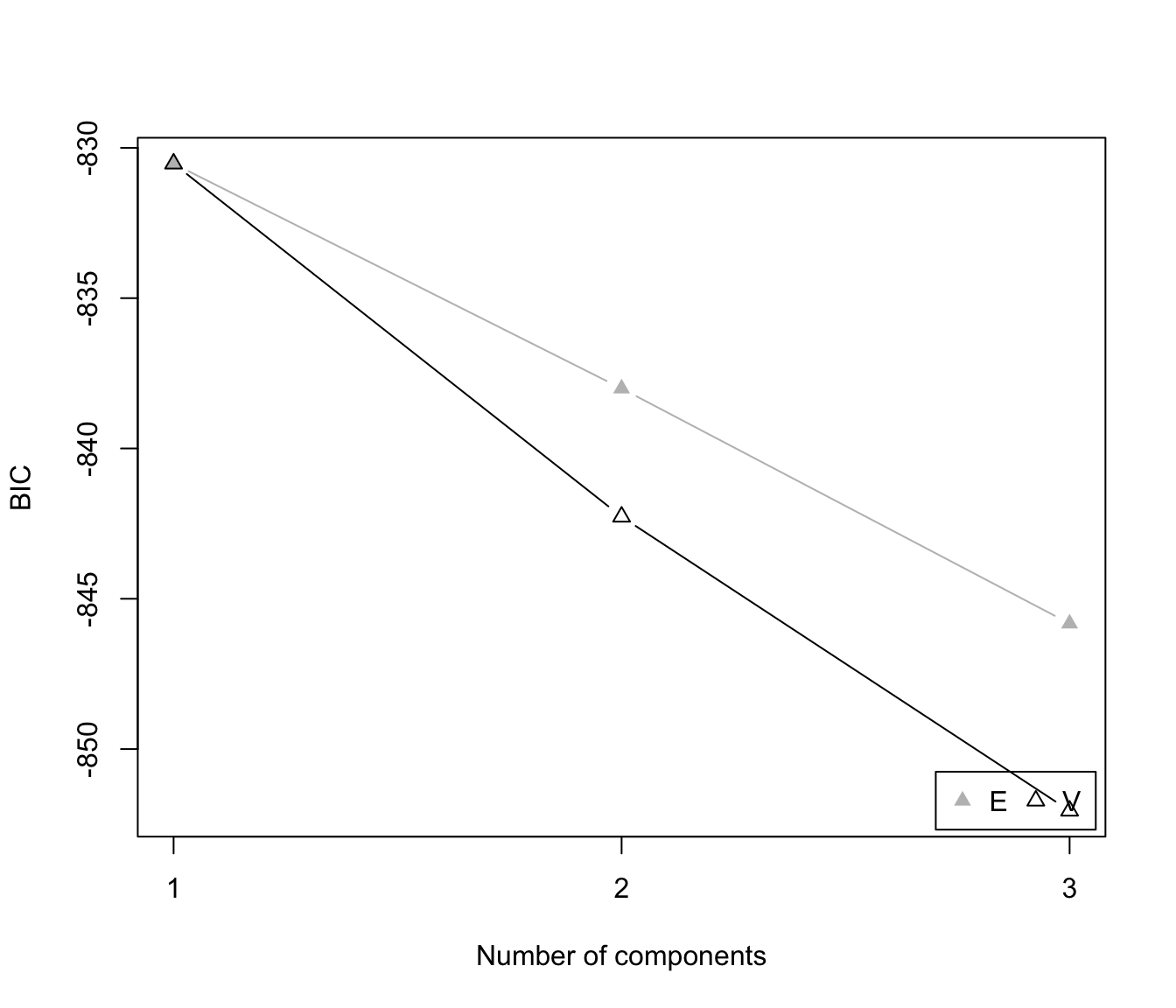
plot(dens, what = "BIC")

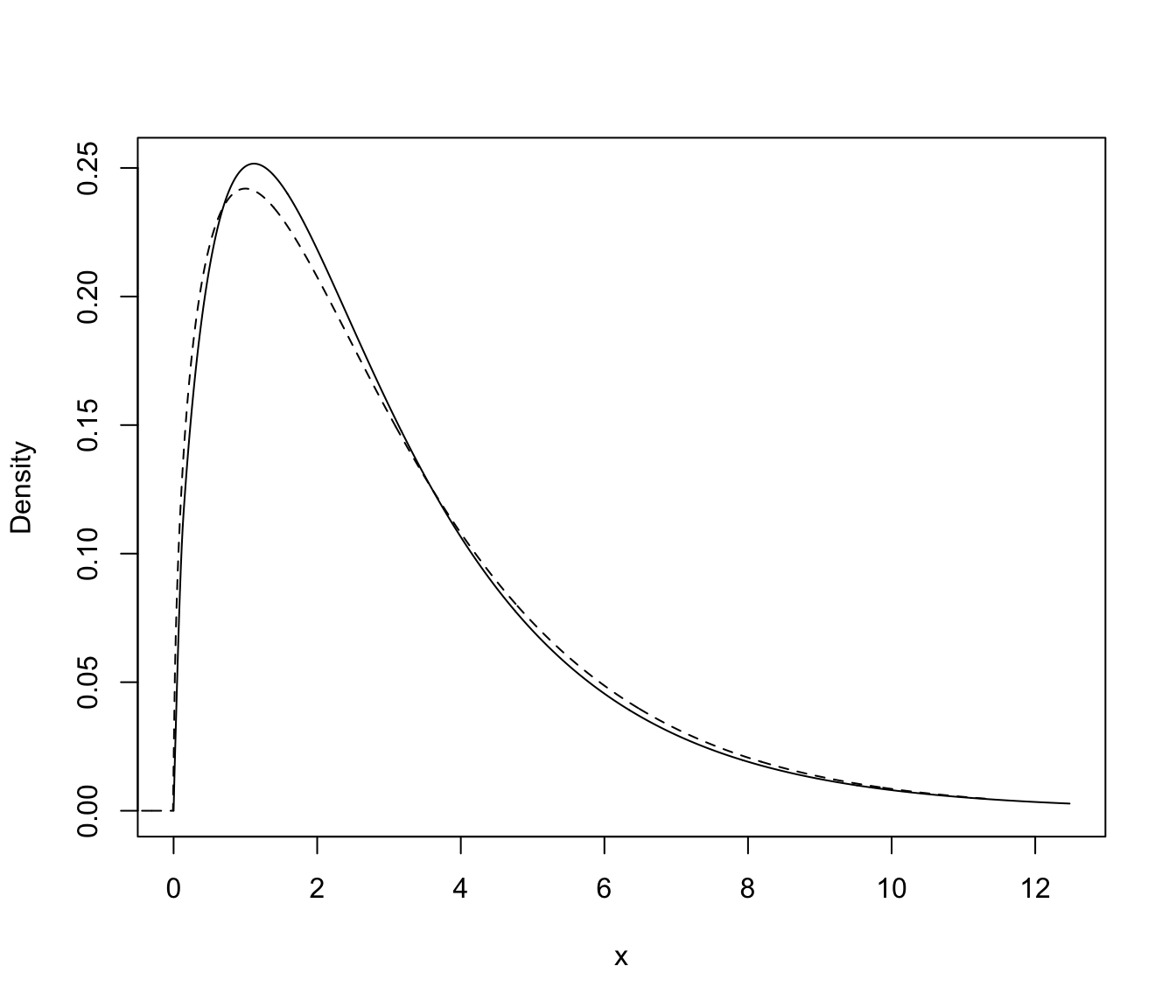
plot(dens, what = "density")
lines(xgrid, f, lty = 2)

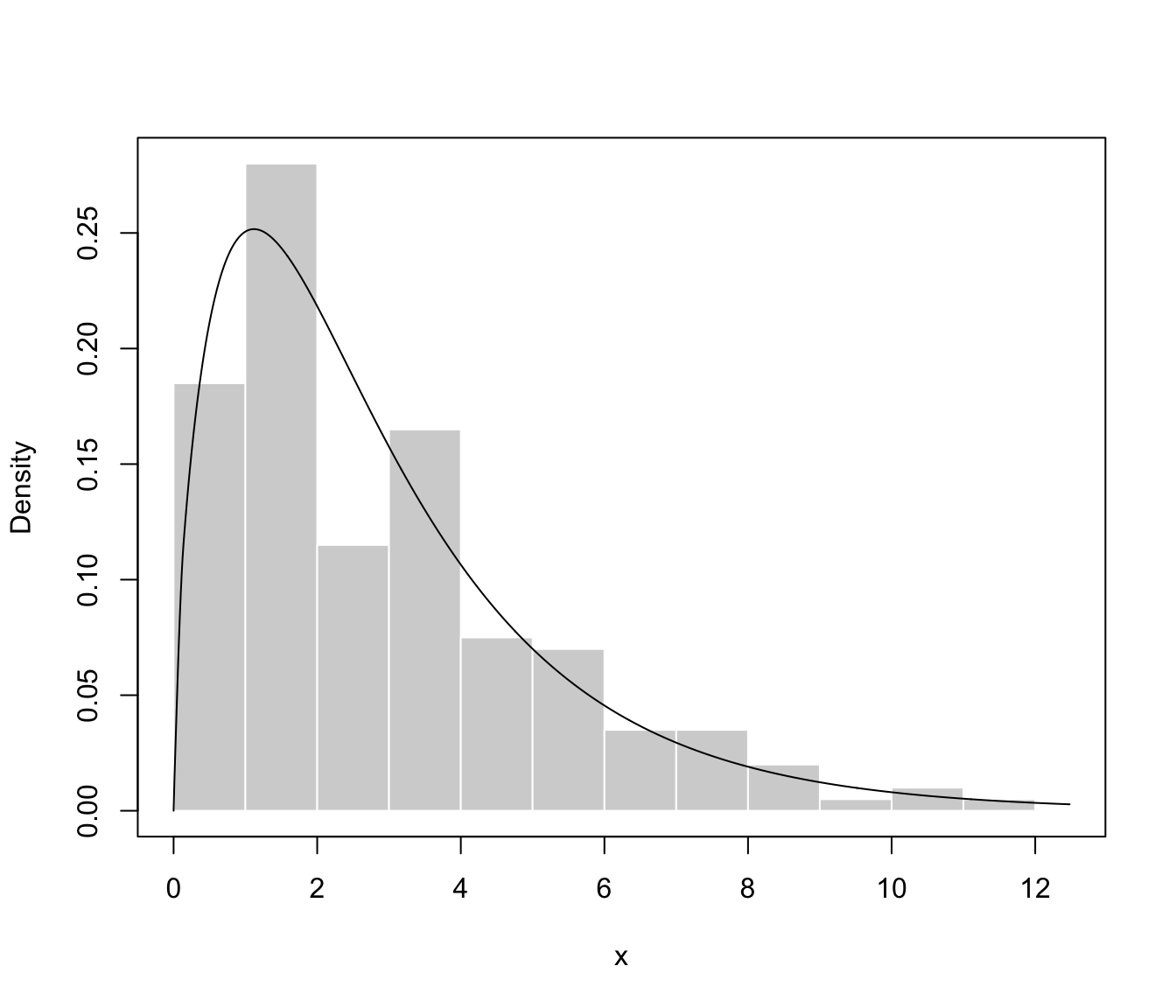
plot(dens, what = "density", data = x, breaks = 15)


# univariate case with lower & upper bounds
x <- rbeta(200, 5, 1.5)
xgrid <- seq(-0.1, 1.1, length=1000)
f <- dbeta(xgrid, 5, 1.5)  # true density
dens <- densityMclustBounded(x, lbound = 0, ubound = 1)
summary(dens)
#> ── Density estimation for bounded data via GMMs ───────────
#>            
#> Boundaries: x
#>       lower 0
#>       upper 1
#> 
#> Model E (univariate, equal variance) model with 1 component
#> on the transformation scale:
#> 
#>  log-likelihood   n df      BIC      ICL
#>        121.0578 200  3 226.2206 226.2206
#> 
#>                                      x
#> Range-power transformation: -0.2071268
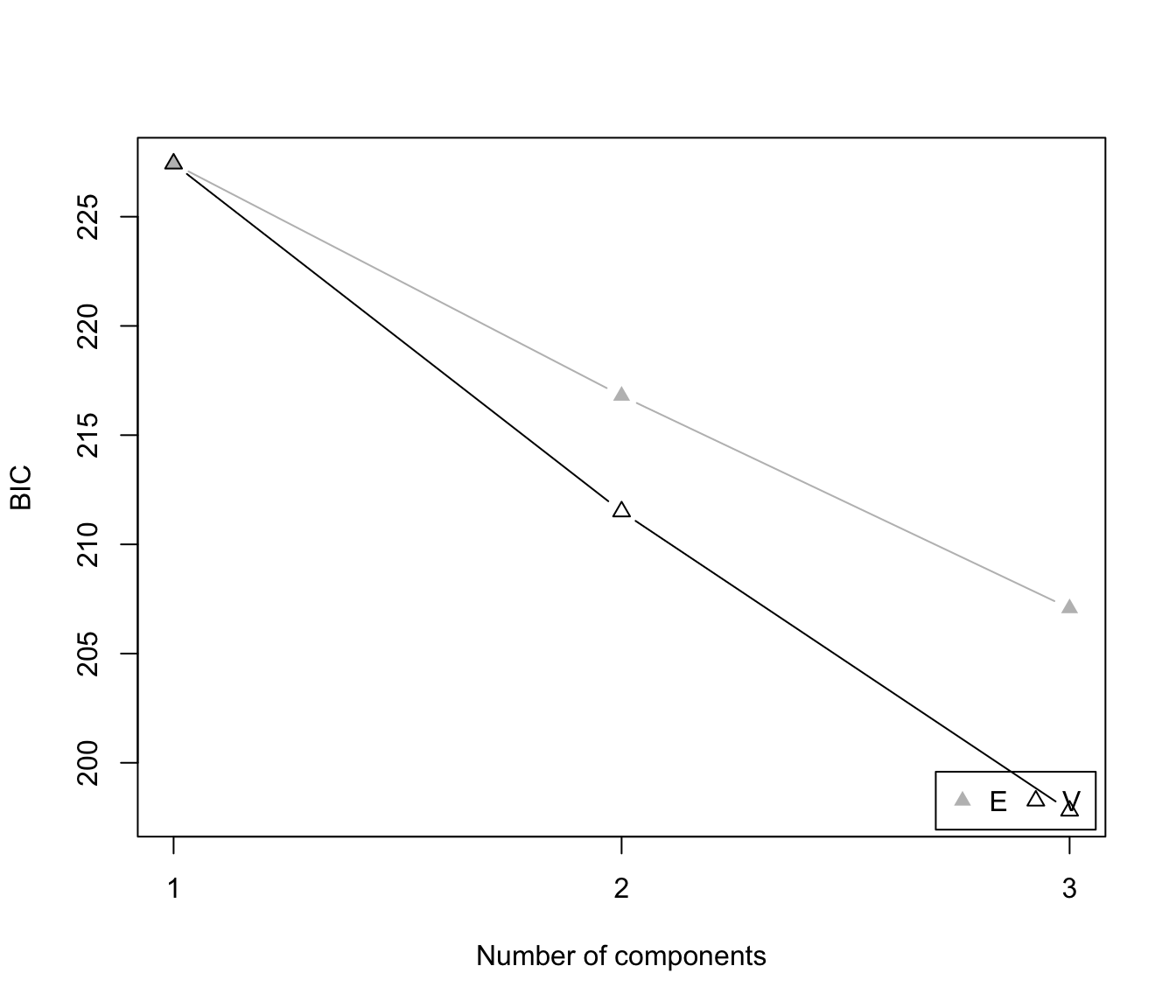
plot(dens, what = "BIC")

plot(dens, what = "density")

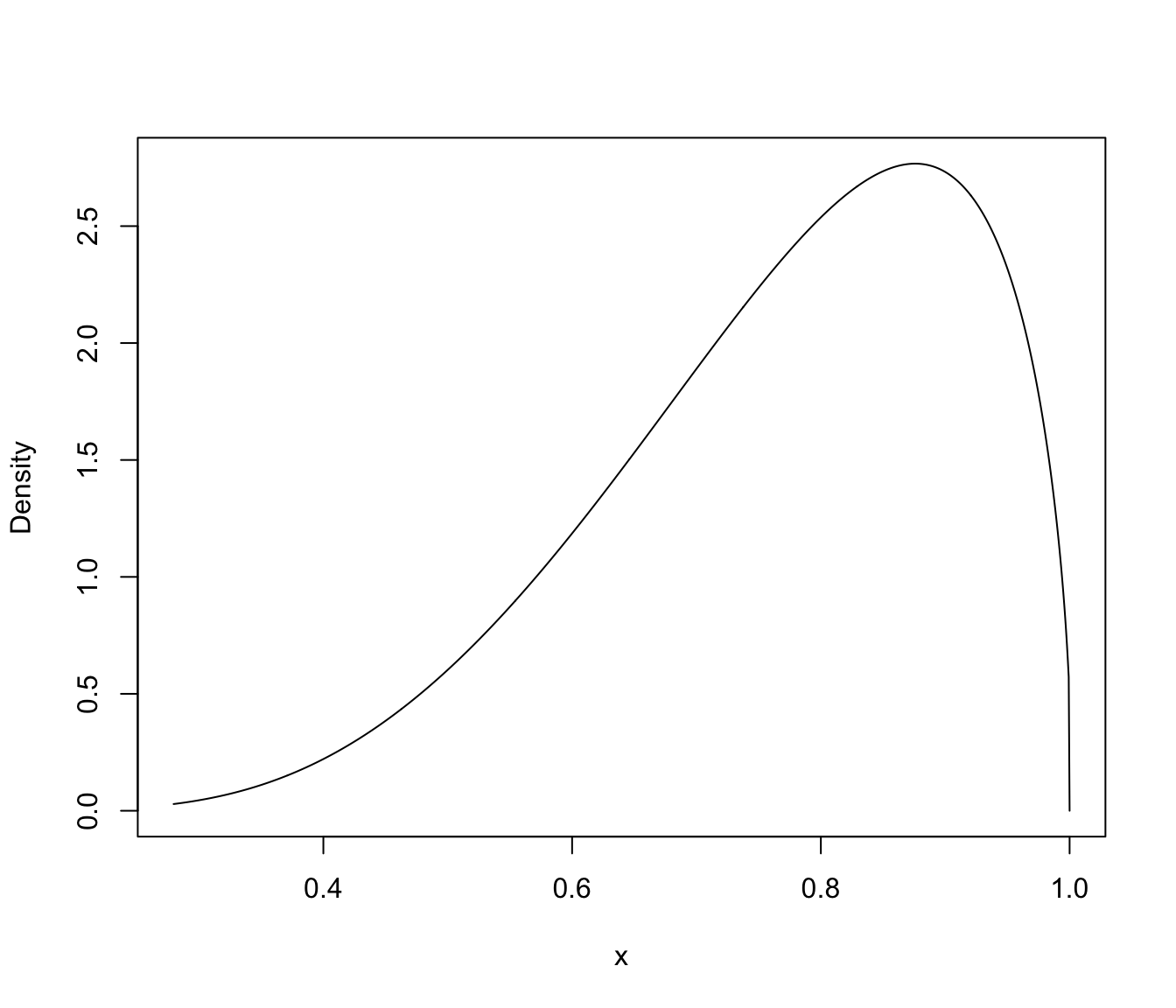
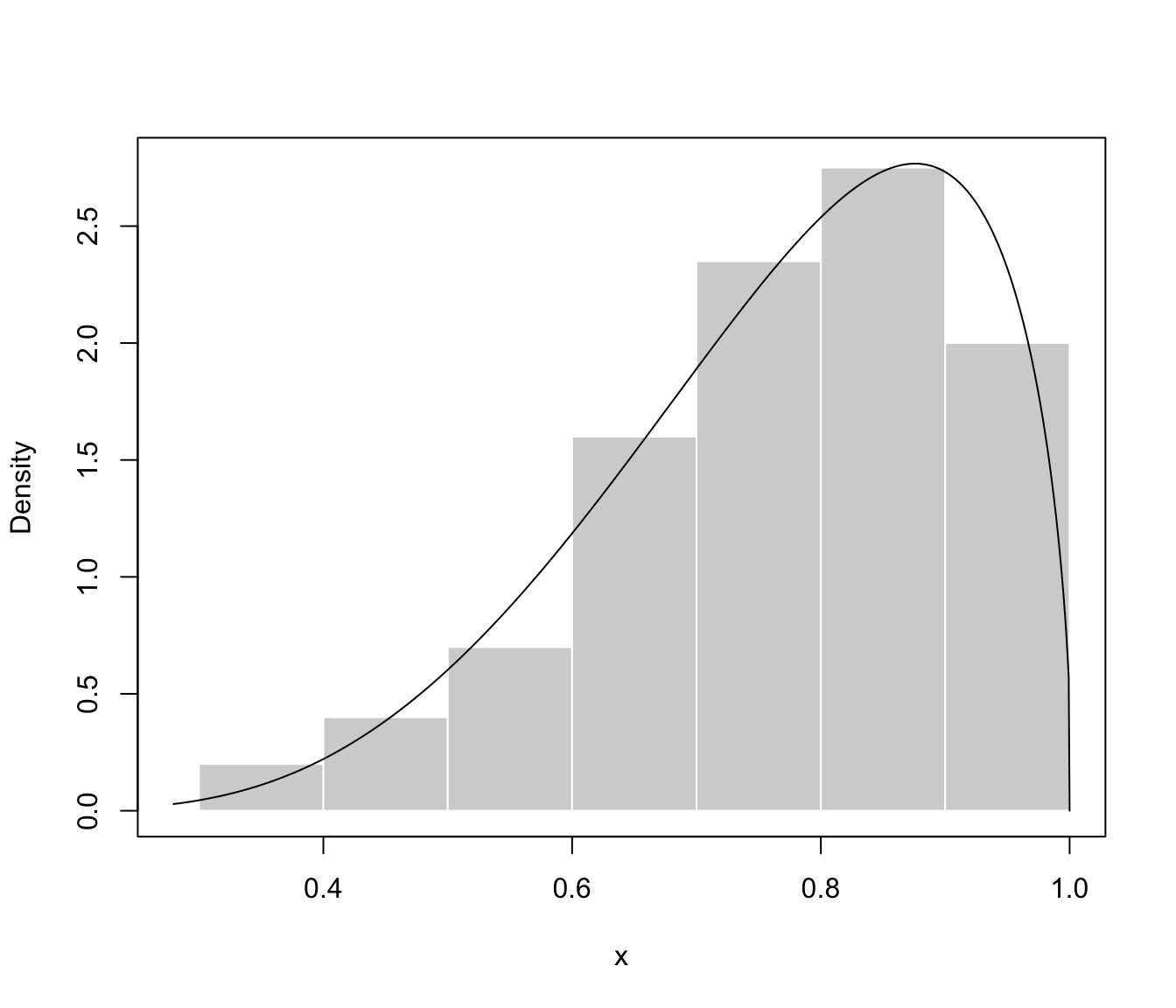
plot(dens, what = "density", data = x, breaks = 9)


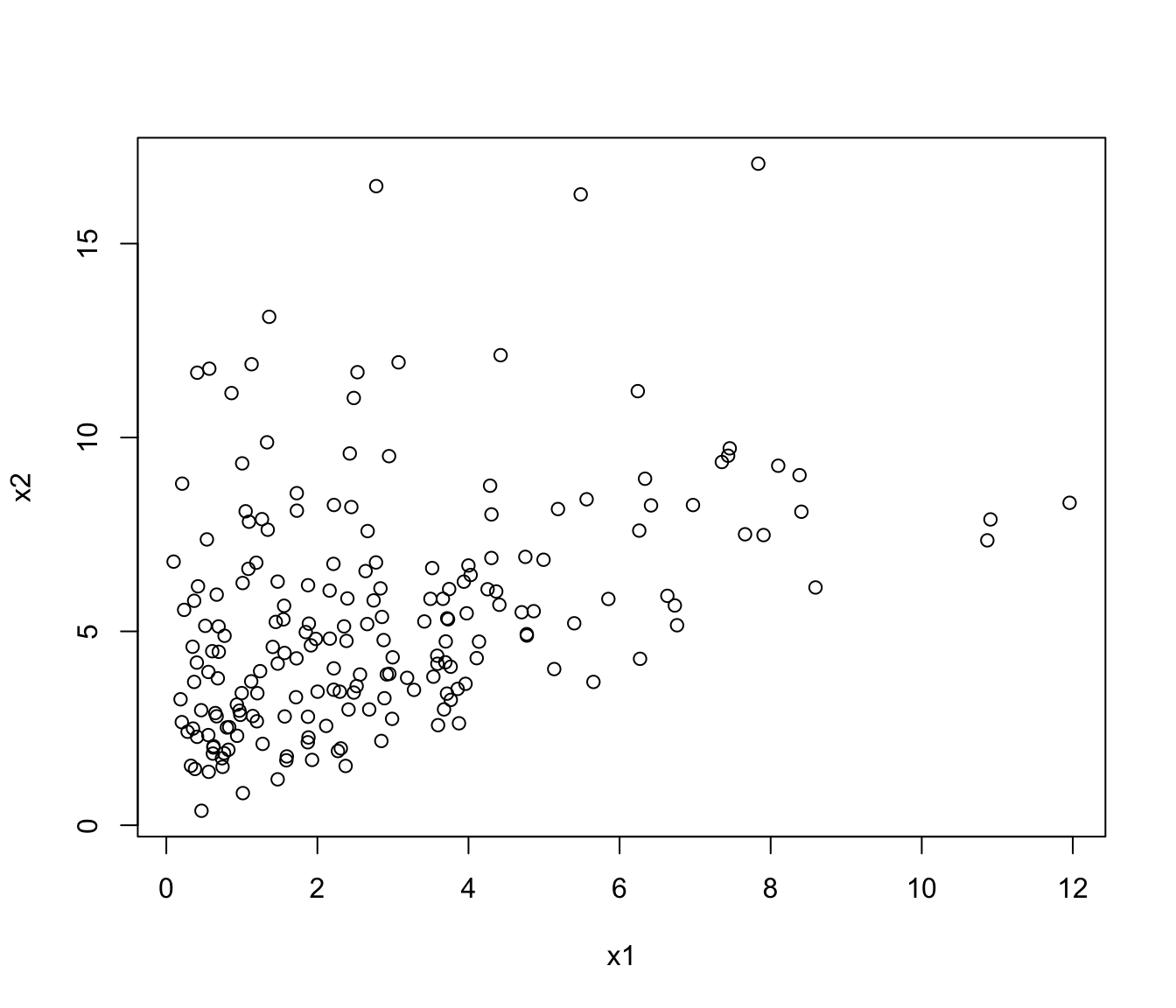
# bivariate case with lower bounds
x1 <- rchisq(200, 3)
x2 <- 0.5*x1 + sqrt(1-0.5^2)*rchisq(200, 5)
x <- cbind(x1, x2)
plot(x)

dens <- densityMclustBounded(x, lbound = c(0,0))
summary(dens, parameters = TRUE)
#> ── Density estimation for bounded data via GMMs ───────────
#>            
#> Boundaries:  x1  x2
#>       lower   0   0
#>       upper Inf Inf
#> 
#> Model VVE (ellipsoidal, equal orientation) model with 1 component
#> on the transformation scale:
#> 
#>  log-likelihood   n df       BIC       ICL
#>       -887.9338 200  7 -1812.956 -1812.956
#> 
#>                                    x1        x2
#> Range-power transformation: 0.2736061 0.3169571
#> 
#> Mixing probabilities:
#> 1 
#> 1 
#> 
#> Means:
#>         [,1]
#> x1 0.8382565
#> x2 2.3483288
#> 
#> Variances:
#> [,,1]
#>           x1        x2
#> x1 1.2897998 0.3371509
#> x2 0.3371509 0.8297843
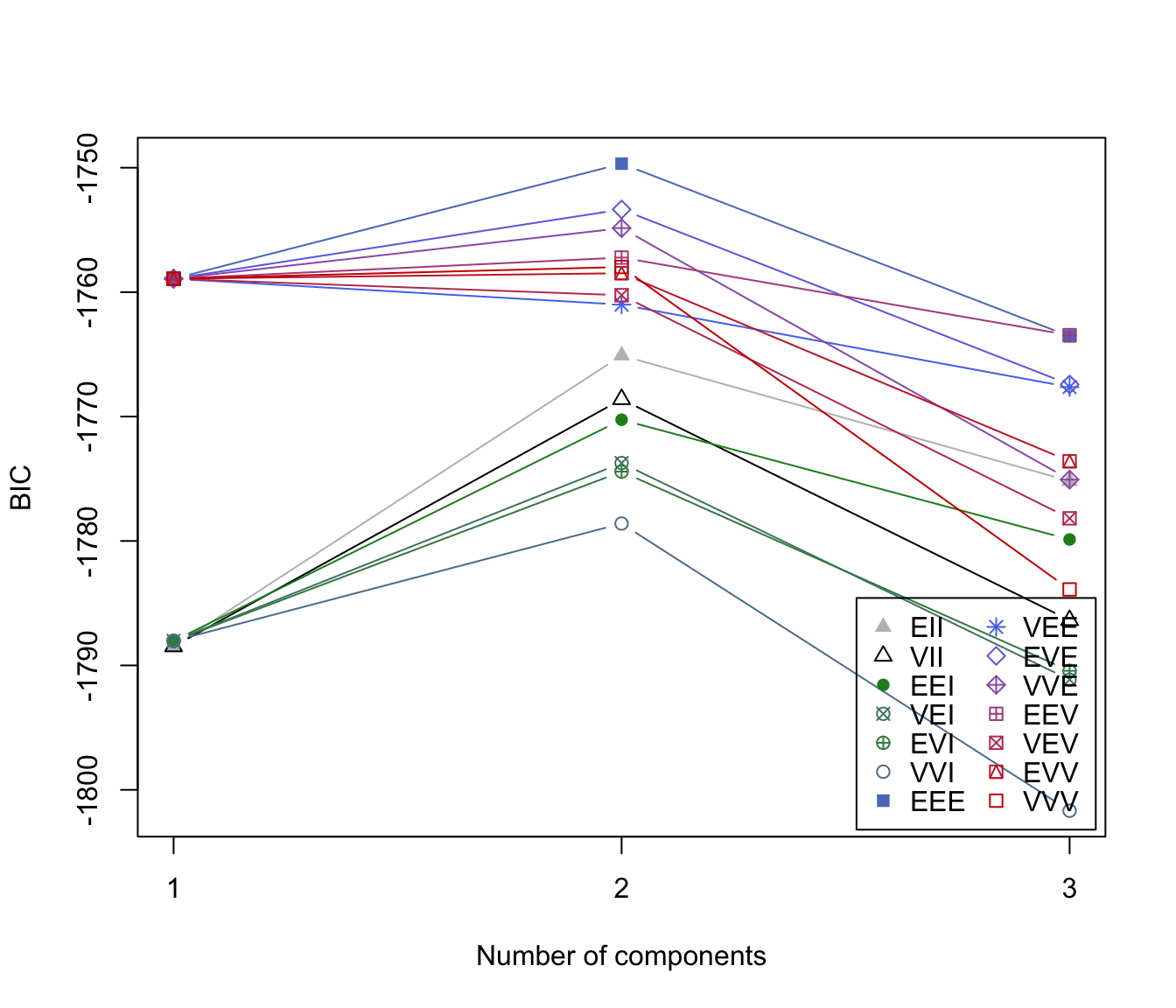
plot(dens, what = "BIC")

plot(dens, what = "density")

plot(dens, what = "density", type = "hdr")

plot(dens, what = "density", type = "persp")

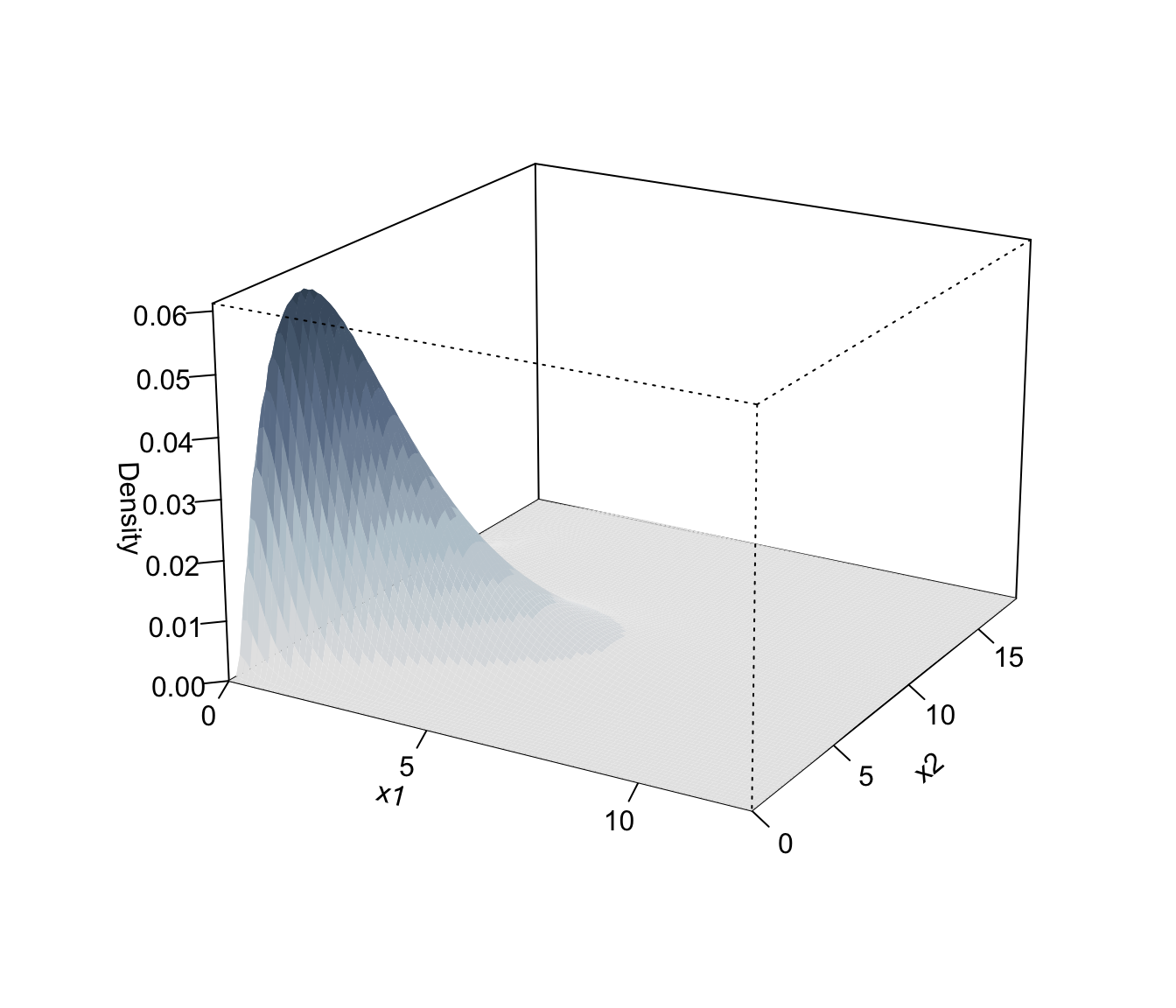# specify different ranges for the lambda values of each variable
dens1 <- densityMclustBounded(x, lbound = c(0,0), 
                              lambda = matrix(c(-2,2,0,1), 2, 2, byrow=TRUE))
# set lambda = 0 fixed for the second variable
dens2 <- densityMclustBounded(x, lbound = c(0,0), 
                              lambda = matrix(c(0,1,0,0), 2, 2, byrow=TRUE))
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...
#> Warning: can't perform marginal optimisation of lambda value(s)...

dens[c("lambdaRange", "lambda", "loglik", "df")]
#> $lambdaRange
#>    [,1] [,2]
#> x1   -3    3
#> x2   -3    3
#> 
#> $lambda
#>        x1        x2 
#> 0.2736061 0.3169571 
#> 
#> $loglik
#> [1] -887.9338
#> 
#> $df
#> [1] 7
#> 
dens1[c("lambdaRange", "lambda", "loglik", "df")]
#> $lambdaRange
#>    [,1] [,2]
#> x1   -2    2
#> x2    0    1
#> 
#> $lambda
#>        x1        x2 
#> 0.2736061 0.3169571 
#> 
#> $loglik
#> [1] -887.9338
#> 
#> $df
#> [1] 7
#> 
dens2[c("lambdaRange", "lambda", "loglik", "df")]
#> $lambdaRange
#>    [,1] [,2]
#> x1    0    1
#> x2    0    0
#> 
#> $lambda
#>        x1        x2 
#> 0.2581141 0.0000000 
#> 
#> $loglik
#> [1] -892.6787
#> 
#> $df
#> [1] 6
#> 
# }