Dimension reduction for model-based clustering and classification

A dimension reduction method for visualizing the clustering or classification structure obtained from a finite mixture of Gaussian densities.

Usage

MclustDR(object, lambda = 1, normalized = TRUE, Sigma,
         tol = sqrt(.Machine$double.eps))

Arguments

object: An object of class 'Mclust' or 'MclustDA' resulting from a call to, respectively, Mclust or MclustDA.
lambda: A tuning parameter in the range [0,1] as described in Scrucca (2014). The directions that mostly separate the estimated clusters or classes are recovered using the default value 1. Users can set this parameter to balance the relative importance of information derived from cluster/class means and covariances. For instance, a value of 0.5 gives equal importance to differences in means and covariances among clusters/classes.
normalized: Logical. If TRUE directions are normalized to unit norm.
Sigma: Marginal covariance matrix of data. If not provided is estimated by the MLE of observed data.
tol: A tolerance value.

Details

The method aims at reducing the dimensionality by identifying a set of linear combinations, ordered by importance as quantified by the associated eigenvalues, of the original features which capture most of the clustering or classification structure contained in the data.

Information on the dimension reduction subspace is obtained from the variation on group means and, depending on the estimated mixture model, on the variation on group covariances (see Scrucca, 2010).

Observations may then be projected onto such a reduced subspace, thus providing summary plots which help to visualize the underlying structure.

The method has been extended to the supervised case, i.e. when the true classification is known (see Scrucca, 2014).

This implementation doesn't provide a formal procedure for the selection of dimensionality. A future release will include one or more methods.

Value

An object of class 'MclustDR' with the following components:

call: The matched call
type: A character string specifying the type of model for which the dimension reduction is computed. Currently, possible values are "Mclust" for clustering, and "MclustDA" or "EDDA" for classification.
x: The data matrix.
Sigma: The covariance matrix of the data.
mixcomp: A numeric vector specifying the mixture component of each data observation.
class: A factor specifying the classification of each data observation. For model-based clustering this is equivalent to the corresponding mixture component. For model-based classification this is the known classification.
G: The number of mixture components.
modelName: The name of the parameterization of the estimated mixture model(s). See mclustModelNames.
mu: A matrix of means for each mixture component.
sigma: An array of covariance matrices for each mixture component.
pro: The estimated prior for each mixture component.
M: The kernel matrix.
lambda: The tuning parameter.
evalues: The eigenvalues from the generalized eigen-decomposition of the kernel matrix.
raw.evectors: The raw eigenvectors from the generalized eigen-decomposition of the kernel matrix, ordered according to the eigenvalues.
basis: The basis of the estimated dimension reduction subspace.
std.basis: The basis of the estimated dimension reduction subspace standardized to variables having unit standard deviation.
numdir: The dimension of the projection subspace.
dir: The estimated directions, i.e. the data projected onto the estimated dimension reduction subspace.

References

Scrucca, L. (2010) Dimension reduction for model-based clustering. Statistics and Computing, 20(4), pp. 471-484.

Scrucca, L. (2014) Graphical Tools for Model-based Mixture Discriminant Analysis. Advances in Data Analysis and Classification, 8(2), pp. 147-165.

Author

Luca Scrucca

Examples

# clustering
data(diabetes)
mod <- Mclust(diabetes[,-1])
summary(mod)
#> ---------------------------------------------------- 
#> Gaussian finite mixture model fitted by EM algorithm 
#> ---------------------------------------------------- 
#> 
#> Mclust VVV (ellipsoidal, varying volume, shape, and orientation) model with 3
#> components: 
#> 
#>  log-likelihood   n df       BIC       ICL
#>       -2303.496 145 29 -4751.316 -4770.169
#> 
#> Clustering table:
#>  1  2  3 
#> 81 36 28 

dr <- MclustDR(mod)
summary(dr)
#> ----------------------------------------------------------------- 
#> Dimension reduction for model-based clustering and classification 
#> ----------------------------------------------------------------- 
#> 
#> Mixture model type: Mclust (VVV, 3) 
#>         
#> Clusters  n
#>        1 81
#>        2 36
#>        3 28
#> 
#> Estimated basis vectors: 
#>              Dir1     Dir2
#> glucose  0.764699  0.86359
#> insulin -0.643961 -0.22219
#> sspg     0.023438 -0.45260
#> 
#>                Dir1      Dir2
#> Eigenvalues  1.2629   0.35218
#> Cum. %      78.1939 100.00000
plot(dr, what = "scatterplot")

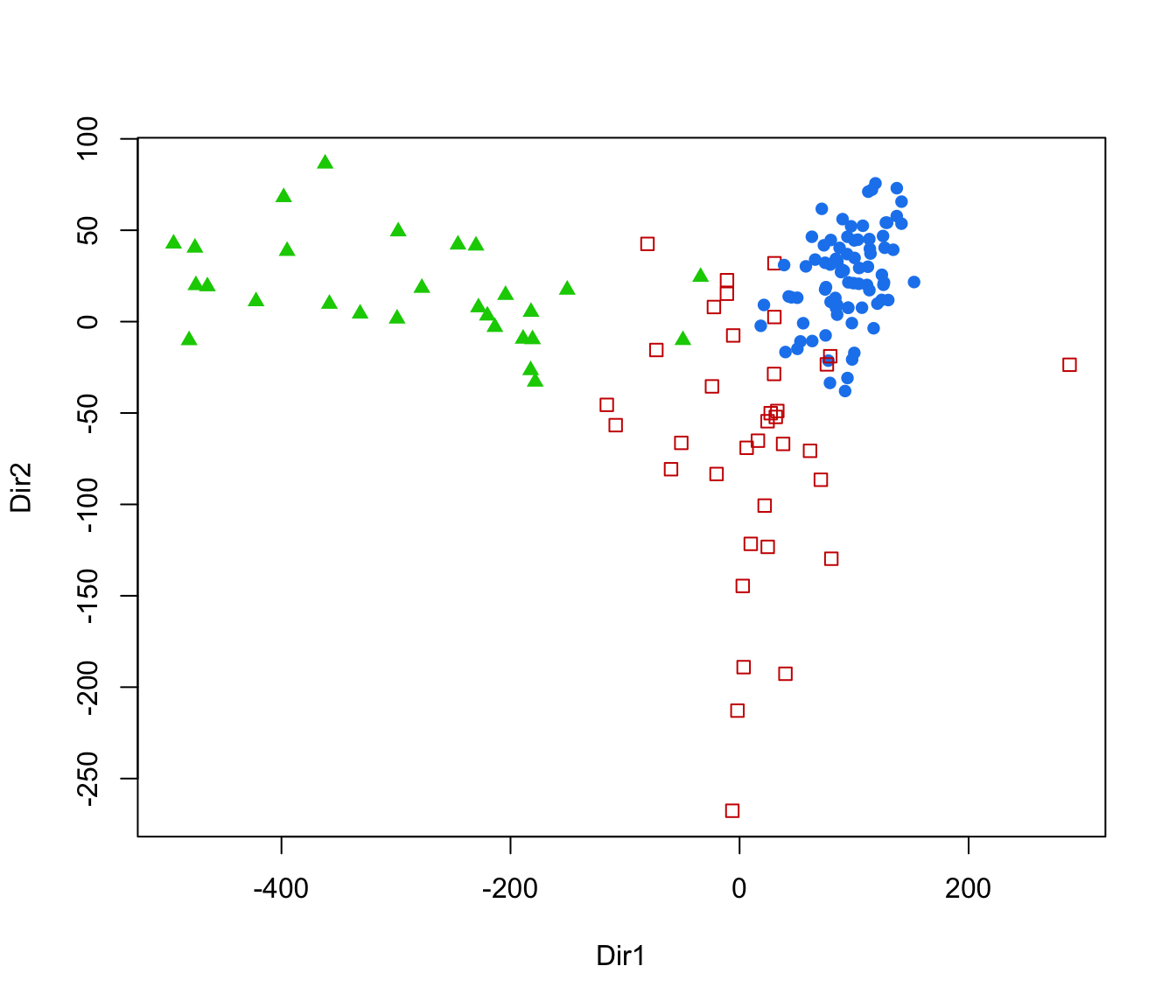plot(dr, what = "evalues")


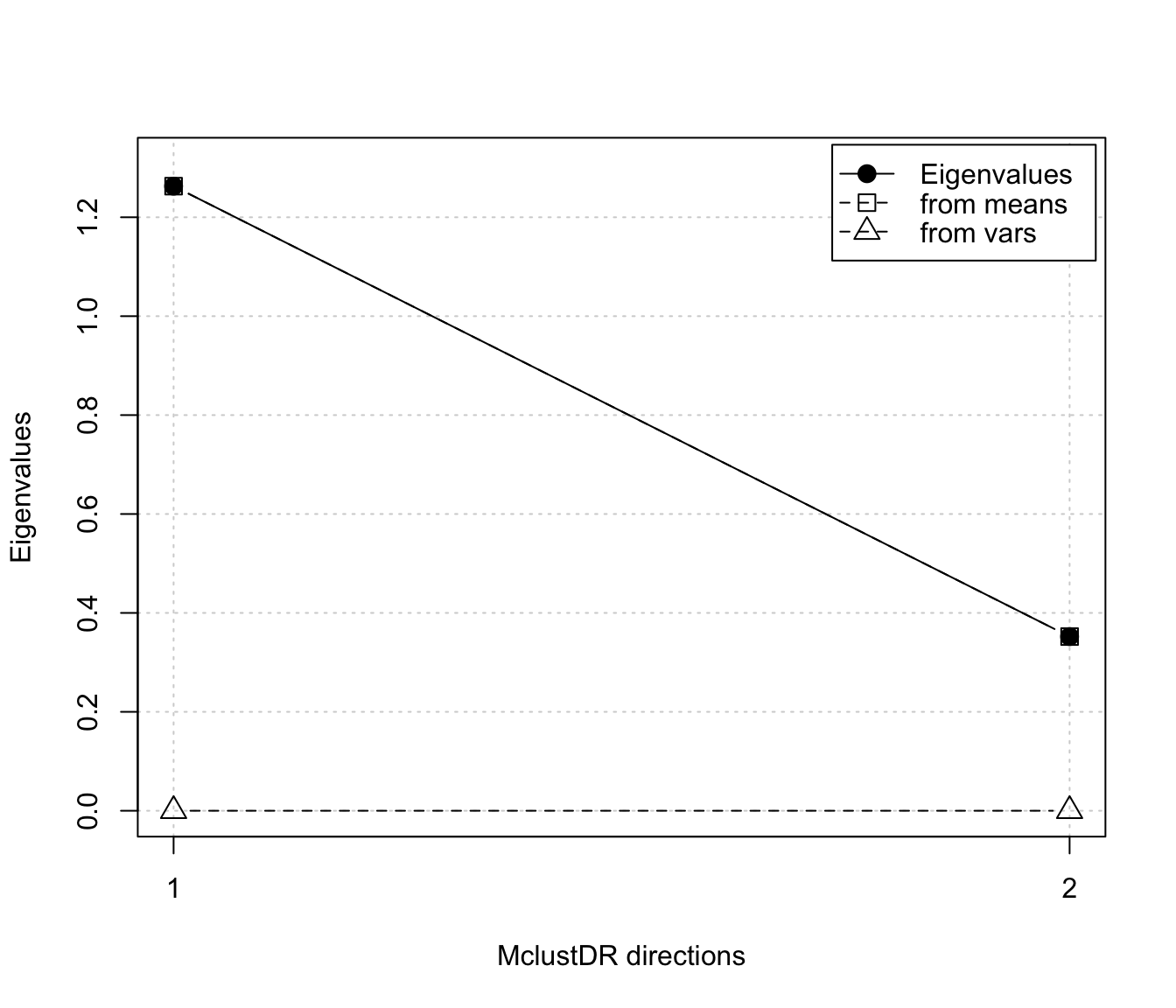dr <- MclustDR(mod, lambda = 0.5) 
summary(dr)
#> ----------------------------------------------------------------- 
#> Dimension reduction for model-based clustering and classification 
#> ----------------------------------------------------------------- 
#> 
#> Mixture model type: Mclust (VVV, 3) 
#>         
#> Clusters  n
#>        1 81
#>        2 36
#>        3 28
#> 
#> Estimated basis vectors: 
#>              Dir1     Dir2      Dir3
#> glucose -0.988671 -0.76532  0.966565
#> insulin  0.142656  0.13395 -0.252109
#> sspg    -0.046689 -0.62955 -0.046837
#> 
#>                Dir1     Dir2      Dir3
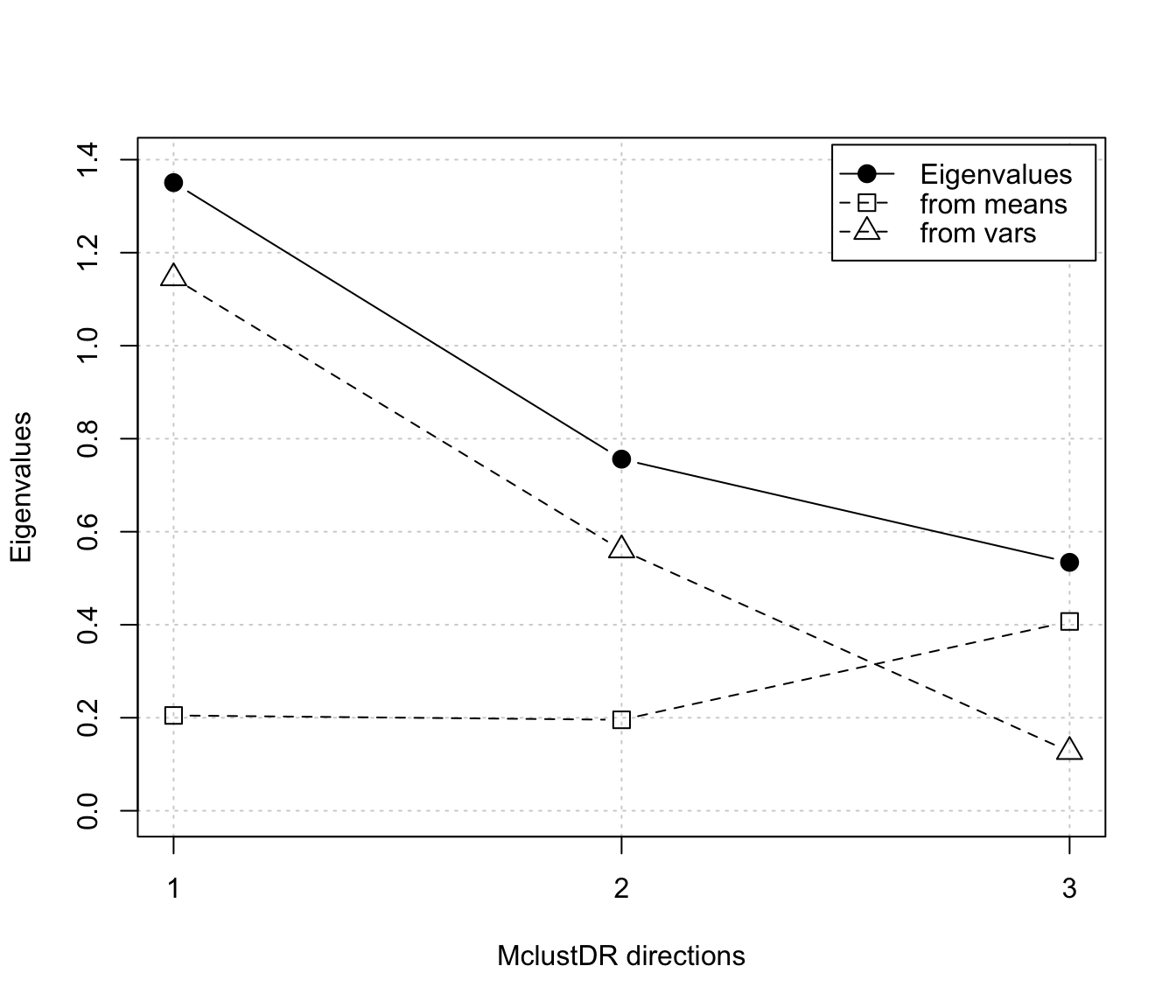
#> Eigenvalues  1.3506  0.75608   0.53412
#> Cum. %      51.1440 79.77436 100.00000
plot(dr, what = "scatterplot")

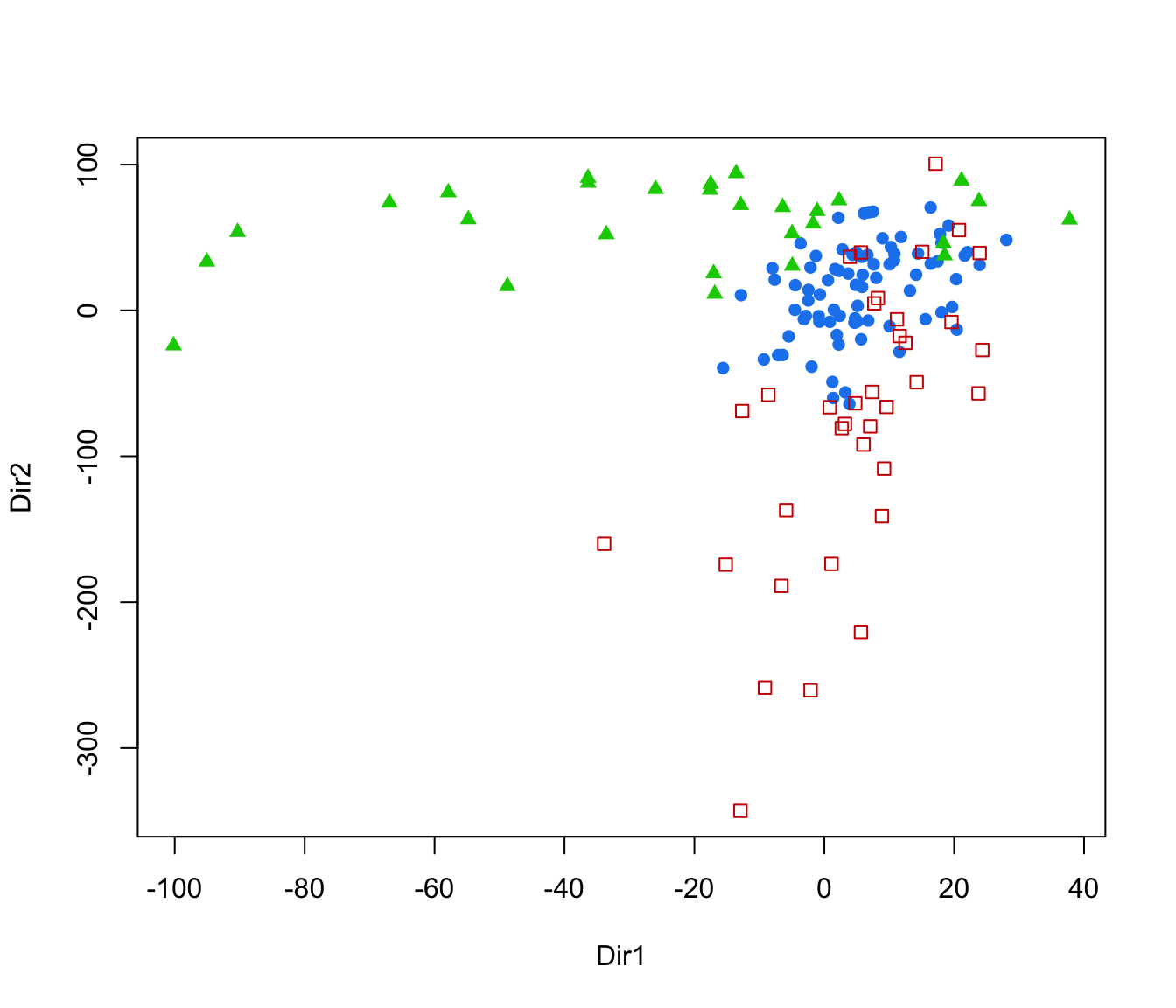plot(dr, what = "evalues")


# classification
data(banknote)

da <- MclustDA(banknote[,2:7], banknote$Status, modelType = "EDDA")
dr <- MclustDR(da)
summary(dr)
#> ----------------------------------------------------------------- 
#> Dimension reduction for model-based clustering and classification 
#> ----------------------------------------------------------------- 
#> 
#> Mixture model type: EDDA 
#>              
#> Classes         n Model G
#>   counterfeit 100   EVE 1
#>   genuine     100   EVE 1
#> 
#> Estimated basis vectors: 
#>                Dir1
#> Length   -0.0019694
#> Left     -0.3271436
#> Right     0.3336519
#> Bottom    0.4391097
#> Top       0.4632982
#> Diagonal -0.6117083
#> 
#>                 Dir1
#> Eigenvalues   1.7081
#> Cum. %      100.0000

da <- MclustDA(banknote[,2:7], banknote$Status)
dr <- MclustDR(da)
summary(dr)
#> ----------------------------------------------------------------- 
#> Dimension reduction for model-based clustering and classification 
#> ----------------------------------------------------------------- 
#> 
#> Mixture model type: MclustDA 
#>              
#> Classes         n Model G
#>   counterfeit 100   EVE 2
#>   genuine     100   XXX 1
#> 
#> Estimated basis vectors: 
#>              Dir1     Dir2
#> Length   -0.07016 -0.25690
#> Left     -0.36888 -0.19963
#> Right     0.29525 -0.10111
#> Bottom    0.54683  0.46254
#> Top       0.55720  0.41370
#> Diagonal -0.40290  0.70628
#> 
#>                Dir1     Dir2
#> Eigenvalues  1.7188   1.0607
#> Cum. %      61.8373 100.0000