Skip to contents

Gaussian Mixture Modelling for Model-Based Clustering, Classification, and Density Estimation

mclust-package.Rd

Gaussian finite mixture models estimated via EM algorithm for model-based clustering, classification, and density estimation, including Bayesian regularization and dimension reduction.

Details

For a quick introduction to mclust see the vignette A quick tour of mclust.

See also:

Author

Chris Fraley, Adrian Raftery and Luca Scrucca.

Maintainer: Luca Scrucca luca.scrucca@unipg.it

References

Scrucca L., Fraley C., Murphy T. B. and Raftery A. E. (2023) Model-Based Clustering, Classification, and Density Estimation Using mclust in R. Chapman & Hall/CRC, ISBN: 978-1032234953, https://mclust-org.github.io/book/

Scrucca L., Fop M., Murphy T. B. and Raftery A. E. (2016) mclust 5: clustering, classification and density estimation using Gaussian finite mixture models, The R Journal, 8/1, pp. 289-317.

Fraley C. and Raftery A. E. (2002) Model-based clustering, discriminant analysis and density estimation, Journal of the American Statistical Association, 97/458, pp. 611-631.

Examples

# \donttest{
# Clustering
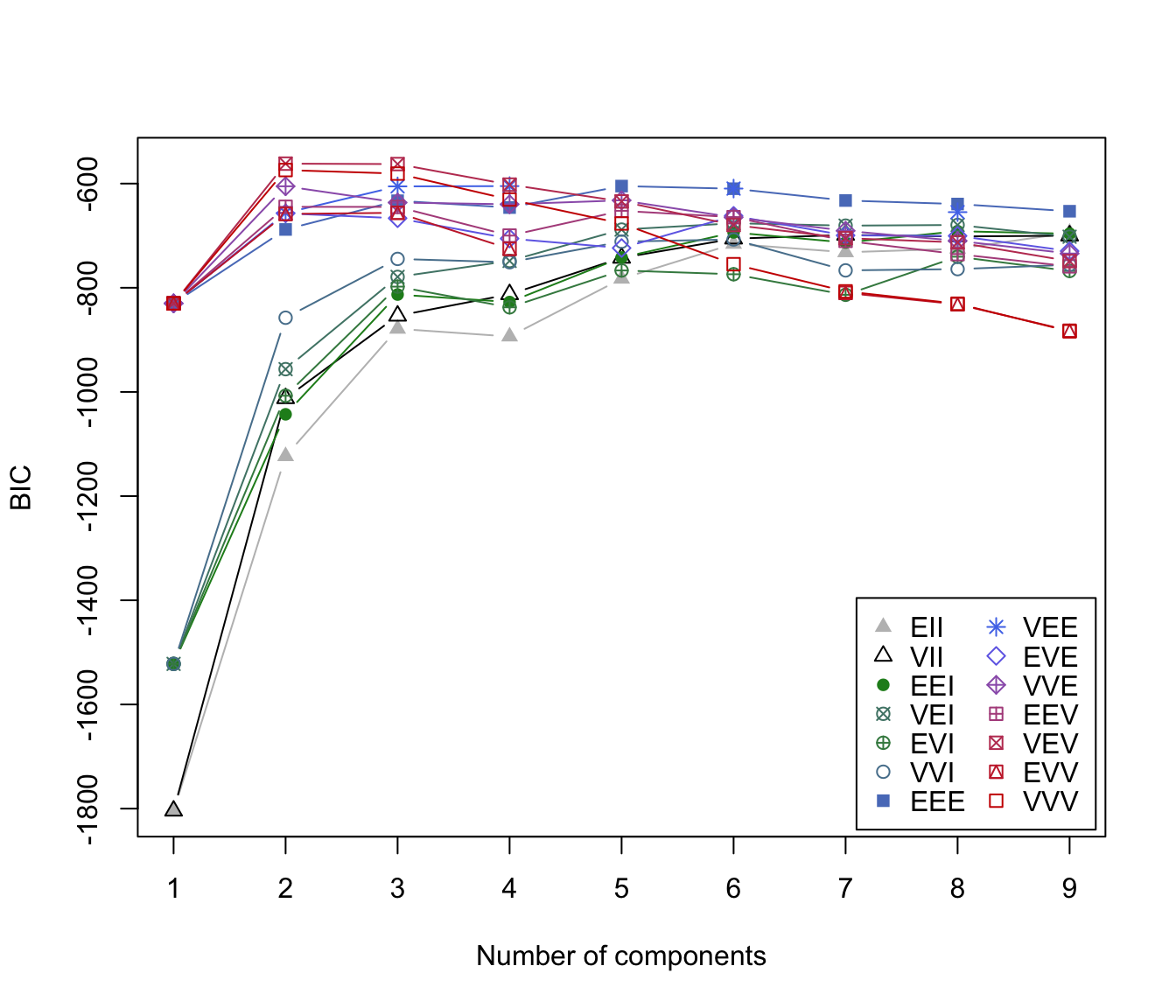
mod1 <- Mclust(iris[,1:4])
summary(mod1)
#> ---------------------------------------------------- 
#> Gaussian finite mixture model fitted by EM algorithm 
#> ---------------------------------------------------- 
#> 
#> Mclust VEV (ellipsoidal, equal shape) model with 2 components: 
#> 
#>  log-likelihood   n df       BIC       ICL
#>        -215.726 150 26 -561.7285 -561.7289
#> 
#> Clustering table:
#>   1   2 
#>  50 100 
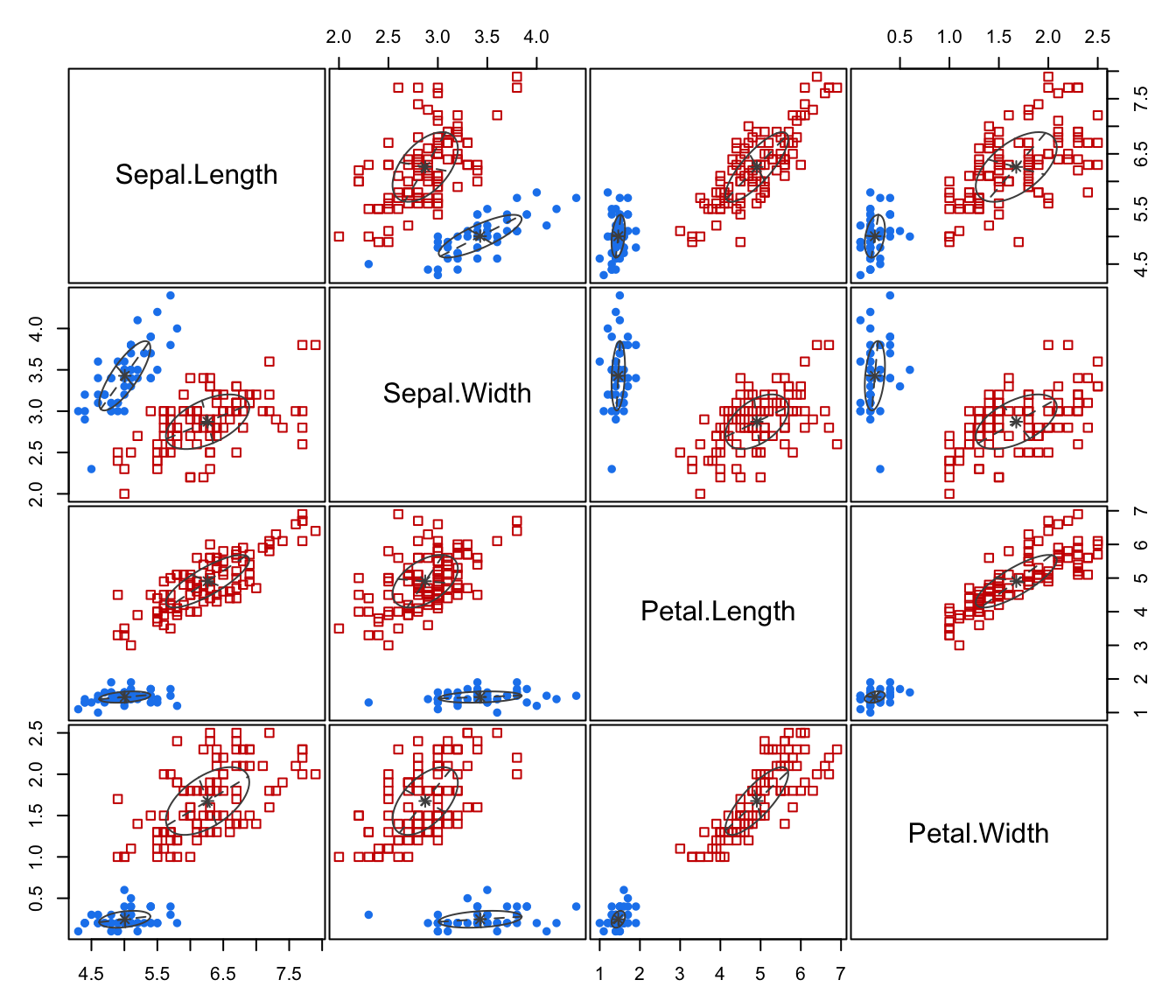
plot(mod1,  what = c("BIC", "classification"))



# Classification
data(banknote)
mod2 <- MclustDA(banknote[,2:7], banknote$Status)
summary(mod2)
#> ------------------------------------------------ 
#> Gaussian finite mixture model for classification 
#> ------------------------------------------------ 
#> 
#> MclustDA model summary: 
#> 
#>  log-likelihood   n df       BIC
#>       -646.0801 200 67 -1647.147
#>              
#> Classes         n  % Model G
#>   counterfeit 100 50   EVE 2
#>   genuine     100 50   XXX 1
#> 
#> Training confusion matrix:
#>              Predicted
#> Class         counterfeit genuine
#>   counterfeit         100       0
#>   genuine               0     100
#> Classification error = 0 
#> Brier score          = 0 
plot(mod2)





# Density estimation
mod3 <- densityMclust(faithful$waiting)

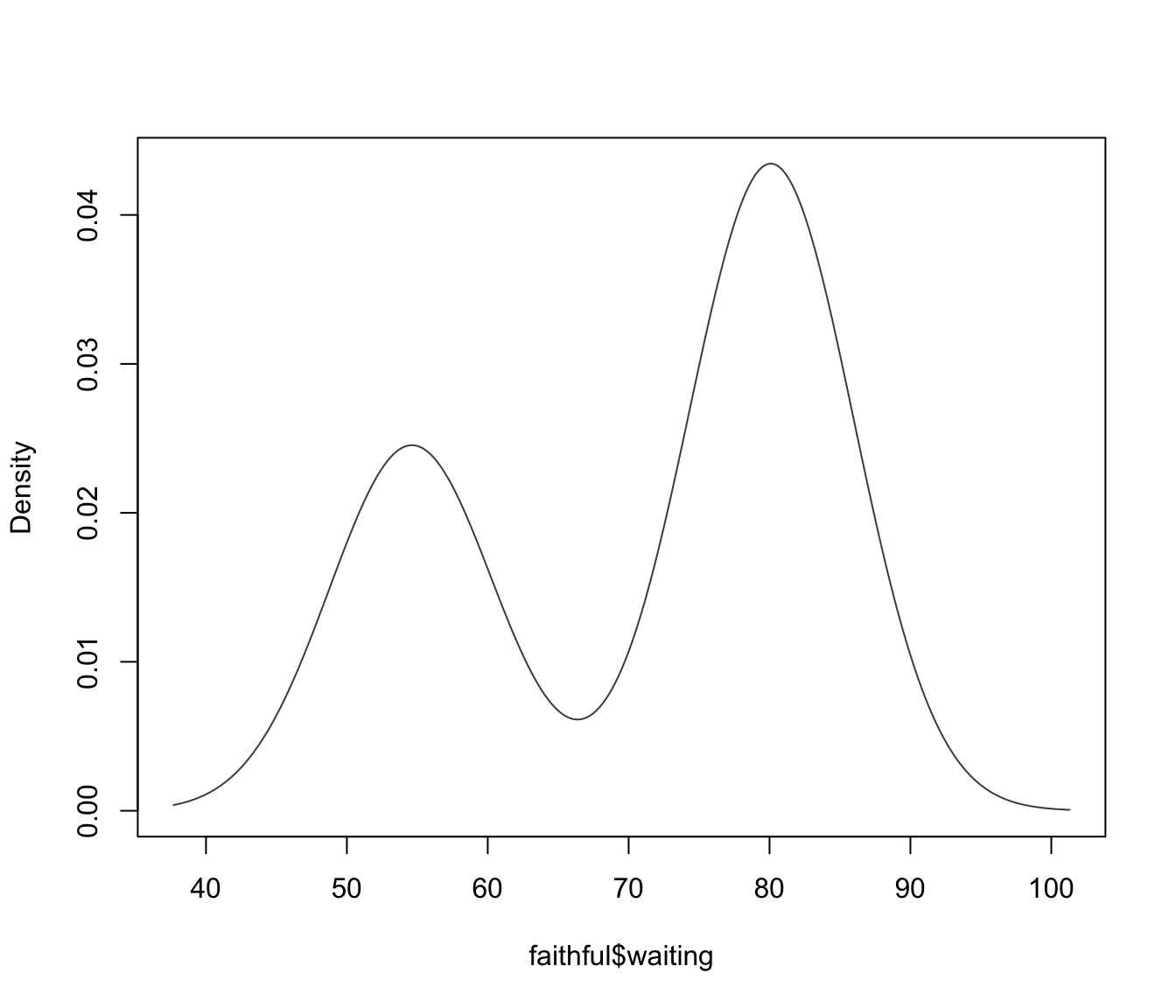summary(mod3)
#> ------------------------------------------------------- 
#> Density estimation via Gaussian finite mixture modeling 
#> ------------------------------------------------------- 
#> 
#> Mclust E (univariate, equal variance) model with 2 components: 
#> 
#>  log-likelihood   n df       BIC       ICL
#>       -1034.002 272  4 -2090.427 -2099.576
# }